Die Fibonacci-Spirale

Weiter geht es in der Blogreihe zur fotografischen Bildgestaltung! Im letzten Beitrag widmeten wir uns dem Goldenen Schnitt, wie wir ihn konstruieren, berechnen und als Gestaltungsraster anwenden können. Heute gehen wir einen Schritt weiter und nehmen uns ein Gestaltungshilfsmittel vor, das eine große Überlappung mit dem Goldenen Schnitt besitzt und gleichzeitig einen gänzlich anderen Ansatz liefert: die Fibonacci-Spirale.

Ein Hauptproblem der meisten Gestaltungsraster

Inzwischen haben wir die Gestaltungsraster der Drittelregel und des Goldenen Schnitts kennengelernt, bei denen wir unser Bildfeld durch horizontale und vertikale Linien gliedern können, auf denen anschließend Motivlinien oder bildwichtige Elemente positioniert werden können.

Diese einfachen Raster zeigen also nur horizontale und vertikale Linien. Und auch wenn wir uns mit Richtungen und Linien erstnoch später in dieser Blogreihe beschäftigen werden, kann so viel schon gesagt werden: Alle Linien, die die Ränder unseres Bildfeldes im rechten Winkel schneiden, werden als recht stativ empfunden. Dies kann für bestimmte Motive natürlich hervorragend, für andere Motiv jedoch völlig unpassend sein.

Die sogenannte Fibonacci-Spirale bietet uns hierbei einen anderen Ansatz. Anstatt uns Linien zu bieten, die parallel zu den Bildrändern sind, beschreibt sie eine Spirale! Nun können wir also Bögen entlang diesesr Gestaltungshilfe positionieren oder bildwichtige Elemente entlang dieser Bögen anordnen.

Aber wieso eigentlich „Fibonacci“ und wieso soll diese Spirale nützlich sein? Leonardo Fibonacci (1170 – 1240) lebte in Pisa und gilt heute als einer der bedeutensten Mathematiker des Mittelalters. Nichtmathematikern ist er jedoch höchstens aus Dan Browns „Sakrileg“ bekannt, in dem die sogenannte „Fibonacci-Reihe“ genannt wird. Fibonacci stieß 1202 auf diese Zahlenreihe, als er das Wachstum einer Kaninchenpopulation beschrieb. Diese Reihe beginnt mit 0 und 1 und besagt, dass wenn man jeweils die beiden vorhergehenden Zahlen addiert, man die darauf folgende erhält:

0	1	1	2	3	5	8	13	21	34	55
		(0+1)	(1+1)	(1+2)	(2+3)	(3+5)	(5+8)	(8+13)	(13+21)	(21+34)

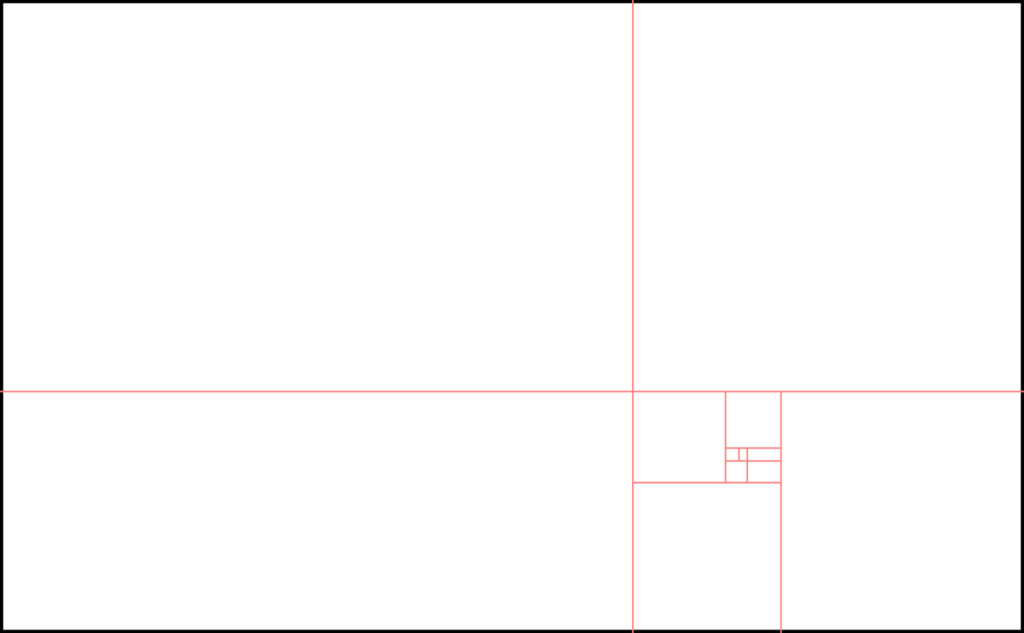
Nun sind wir immer noch nicht schlauer, was uns das im Bezug auf die Bildgestaltung helfen soll. Aber Forschungen haben ergeben, dass viele Wachstumsverhältnisse in der Natur einer ähnlichen Reihung folgen. Und wenn wir mal die beiden Zahlen, die die folgende ergeben, dividieren, nähern wir uns sehr schnell einer bereits bekannten Zahl an: 1,618 (z.B. 55/34=1,6176). Aufmerksame Leser des Blogs sollten nun bemerken, dass es sich hierbei um den Goldenen Schnitt handelt – und somit haben wir den ersten Bezug zur Bildgestaltung! Wenn man die oben gezeigte Zahlenreihe als Quadrate mit der jeweiligen Kantenlänge darstellt, kann man ein Gestaltungsraster entwerfen, das Parallelen mit dem Goldenen Schnitt aufweist:

Die zwei Linien, die die gesamte Bildfläche schneiden, sind die rechte und untere Gestaltungslinie unseres Goldenen-Schnitt-Rasters. Super – aber wieder nur Linien, die die Bildränder im rechten Winkel schneiden und somit als statisch empfunden werden.

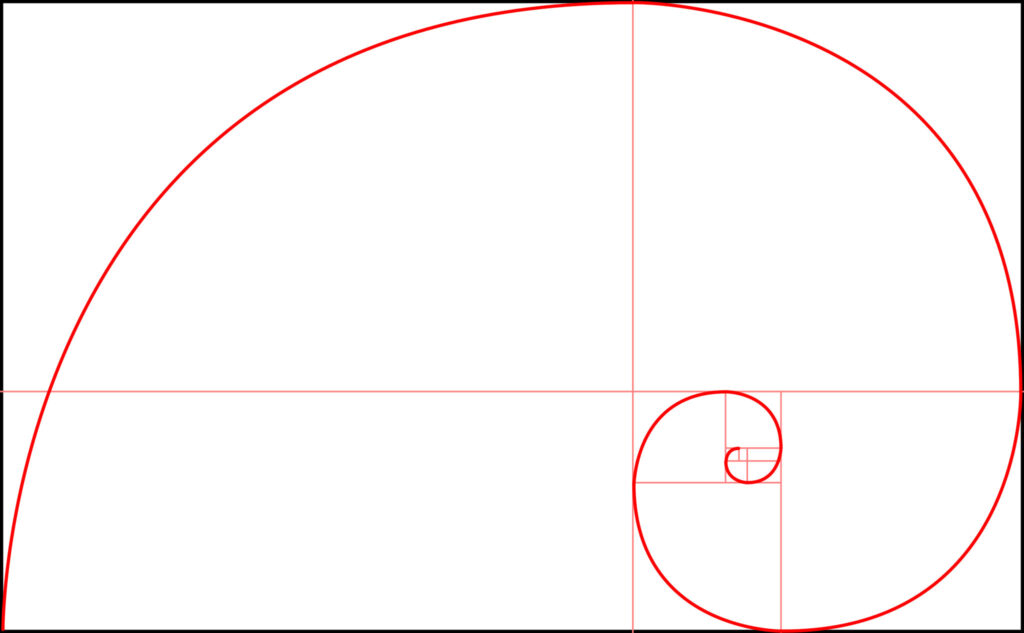
Zieht man nun allerdings in jedem Quadrat einen Viertelkreis und verbindet diese, erhalten wir die oben gezeigte Spirale, die sich theoretisch immer weiter fortführt.

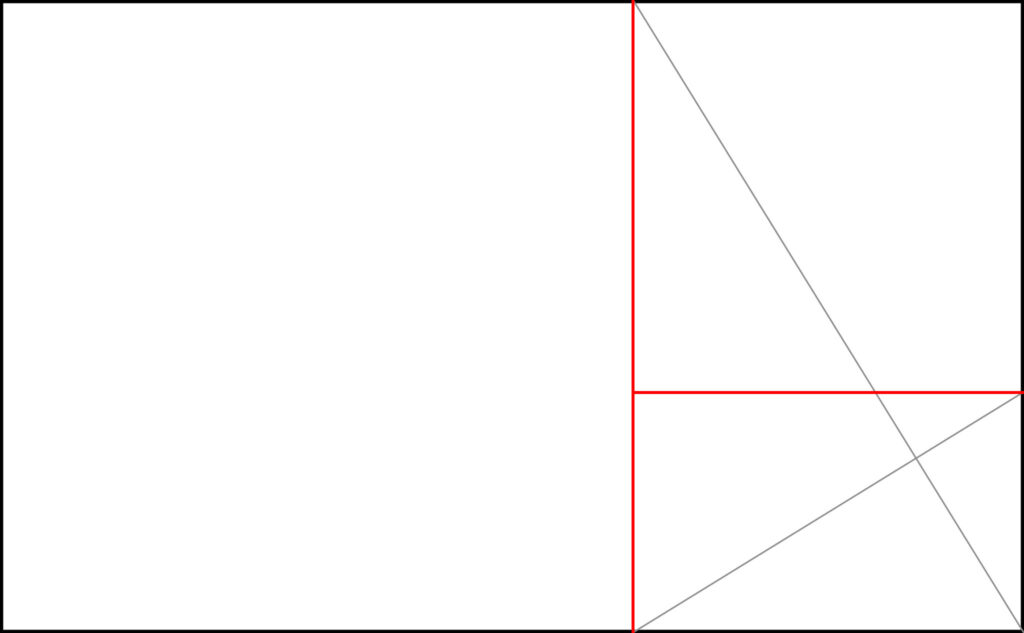
Konstruieren kann man dieses Raster auch, ähnlich dem Goldenen Schnitt. Man zieht zunächst eine Diagonale und zieht anschließend eine Schräge aus der leeren Ecke, die die Diagonale im rechten Winkel schneidet (eine sogenannte Gegendiagonale). Wo diese Linie den Bildrand trifft, ziehen wir Vertikale – voilà, unsere rechte Teilungslinie des Goldenen Schnitts. Nun haben wir ein neues Rechteck erhalten, in dem wir genau gleich verfahren können. Eine Diagonale haben wir ja bereits, also noch eine Linie aus der Ecke, die sie im rechten Winkel schneidet. Wo sie auf den Bildrand trifft, entsteht die nächste Rasterlinie usw.

Die Fibonacci-Spirale in Anwendung:

Wie bereits gesagt, können nun Elemente entlang der Kurve angeordnet oder auch im Zentrum der Spirale positioniert werden.

Wie alle Gestaltungsraster kann man die Fibonacci-Spirale natürlich auch im Hochformat anwenden:

Wer sich jetzt wundert, dass das Raster, was ich über diese Bilder überlagert habe, nicht das gesamte Bildfeld ausfüllt: Ich habe mich bei der Überlagerung an die korrekte Spirale mit einem Seitenverhältnis von 1:1,618 gehalten und diese über diese 2:3-Bilder gelegt. Wer sich die Spirale in Lightroom als Freistellungsüberlagerung anzeigen lässt, erhält die auf die jeweilige Bildfläche transformierte Variante der Spirale. Solltet ihr die Fibonacci-Spirale als Freistellungsüberlagerung in Lightroom nicht sehen, könnt ihr die Überlagerung mit der Taste „o“ durchschalten bzw. mit „cmd+o“ drehen.

Auch wenn die Fibonacci-Spirale einige Überlappung mit dem Goldenen Schnitt hat, erlaubt sie uns doch auch eine viel dynamischere Komposition entlang der Kurve. Wenn wir unser Hauptmotiv oder Fokuszone in das Zentrum der Spirale legen, schieben wir unser Motiv weiter aus der Bildmitte heraus, als dies im Goldenen Schnitt der Fall wäre. Das kann hervorragend sein, um die Bildfläche besser auszunutzen, kann aber auch schneller zu unausgewogenen Kompositionen führen, wenn der gesamte Bildinhalt nur in der Spirale sitzt. Probiert es einfach aus!

Martin